Observación Planetaria
Autor: Enzo De BernardiniPlanetas
Mercurio Venus Marte Júpiter Saturno Urano NeptunoGeneralidades
Los planetas son con seguridad los cuerpos mas interesantes de observar del Sistema Solar, junto con la Luna y el Sol. Para localizar un planeta es necesario saber que siempre se desplazan en las proximidades de la eclíptica; esto es debido a que la inclinación de la órbita no difiere mucho con la de la Tierra (el plano del Sistema Solar) Las constelaciones que atraviesa la eclíptica son principalmente las zodiacales y varias secciones de otras cercanas a estas. En la mayoria de los mapas y atlas se en encuentra marcada la eclíptica.
Para saber donde buscar: la altura máxima (en el meridiano, línea norte-sur que pasa por el cenit) sobre el horizonte de la eclíptica varía según la posición del observador y la época del año. Para calcularla y saber identificar la zona por donde se mueven los planetas, diríjase a la sección de coordenadas. Una primer referencia es saber que la Luna se mueve en las cercanías de la eclíptica. Los planetas se localizan sobre la línea relativamente cercana que forman los puntos este-oeste y la altura de la Luna.
Los planetas de nuestro Sistema Solar se dividen en dos grandes grupos, los inferiores y los superiores, según se encuentren en una órbita interna o externa con respecto a la de la Tierra respectivamente. Los planetas inferiores son: Mercurio y Venus, y los superiores: Marte, Júpiter, Saturno, Urano, Neptuno y Plutón. Varios de estos son visibles a simple vista, solo hay que saber cuando y donde mirar.
En la observación de planetas interiores, uno de los factores a tener en cuenta es la elongación, esto es, la distancia angular entre el Sol y el planeta. Este ángulo es decisivo, dado que si es muy pequeño el planeta se encuentra demasiado cerca del Sol como para ser encontrado y observado.
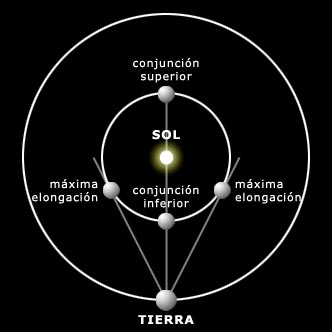
En el gráfico superior se detallan los puntos de máxima elongación, los momentos en que la distancia angular entre el Sol y el planeta son máximas.
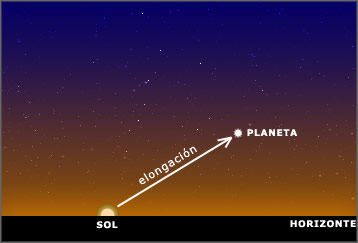
En el caso de los planetas exteriores, las condiciones geométricas a tener en cuenta son dos: la oposición y la cuadratura.
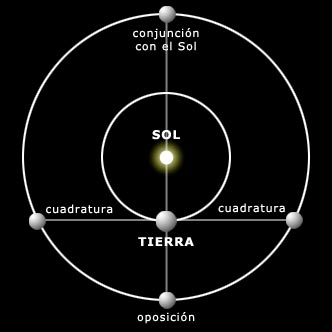
Tal como muestra el gráfico superior, la oposición se produce cuando el sistema Sol-Tierra-planeta quedan alineados. Las cuadraturas son los puntos en los que la elongación es de 90 grados.
Para observar planetas, sobre todo los brillantes (Mercurio, Venus, Marte, Júpiter y Saturno) se recomienda utilizar oculares de distancias focales cortas, para tener la máxima ampliación. No debe sobrepasarse las ampliaciones adecuadas para cada equipo, es mas conveniente sacrificar algo de aumento en pro de la nitidez de imagen.
Dependiendo de las condiciones geómetricas (de las posiciones relativas de la Tierra, el Sol y el planeta) también dependen la fase, el tamaño angular y la magnitud (brillo).
La fase se suele medir en fracción o en porcentaje. En el primer caso se mide de 0 a 1, una fase de 1.0 equivale a llena y una de 0.0 a nueva. Un valor de 0.5 corresponde a un cuarto. En caso de medirse en porcentaje, es similar: 100% equivale a una fase llena, 0% a una fase nueva, con sus intermedio: 50% para los cuartos.
Los planetas que más cambios de fases presentan son los interiores: Mercurio y Venus. En los momentos cercanos a la conjunción superior la fase en máxima, y en los cercanos a la conjunción inferior es mínima. En las elongaciones máximas la fase es del 50%, menguando si se dirige hacia la conjunción inferior y creciendo si se derige a la conjunción superior.
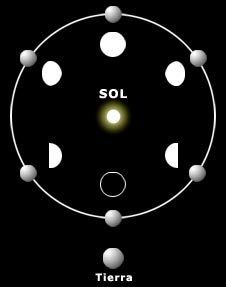
El tamaño angular varía con la distancia al planeta. Se mide en segundos de arco (la esfera celeste se extiende por 360 grados, y se divide en grados minutos y segundos) y es máxima cuando el planeta se localiza más cerca de la Tierra.
Otra característica de los planetas, y de todo cuerpo que órbita a otro, son las posiciones extremas de la órbita, los puntos más cercanos y lejanos al cuerpo orbitado. En el caso de orbitar al Sol (planetas, asteroides, cometas) se denomina perihelio al punto más cercano y afelio al más lejano de la órbita.
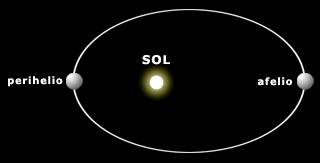
La diferencia entre la distancia del perihelio y el afelio depende de la excentricidad orbital, el grado de "achatamiento" de la órbita respecto de una circular. La excentricidad orbital se mide desde 0 a 1, correspondiendo 0 a órbitas circulares.
Leyes de Kepler
El astrónomo alemán Johannes Kepler (1571-1630) formuló las tres famosas leyes que llevan su nombre después de analizar un gran número de observaciones realizadas por Tycho Brahe (1546-1601) de los movimientos de los planetas, sobre todo de Marte.
Kepler, haciendo cálculos sumamente largos, encontró que había discrepancias entre la trayectoria calculada para Marte y las observaciones de Tycho, diferencias que alcanzaban en ocasiones los 8 minutos de arco (las observaciones de Tycho poseían una exactitud de alrededor de 2 minutos de arco)
Estas diferencias lo llevaron a descubrir cual era la verdadera órbita de Marte y los demás planetas del Sistema Solar.
1ra Ley - Órbitas Elípticas
Las órbitas de los planetas son elipses que presentan una pequeña excentricidad y en donde el Sol se localiza en uno de sus focos.
Puede imaginarse una elipse como un círculo aplastado. Formalmente se denomina elipse a una curva plana y cerrada en donde la suma de la distancia a los focos (puntos fijos, F1 y F2) desde uno cualquiera de los puntos M que la forman es constante e igual a la longitud del eje mayor de la elipse (segmento AB). El eje menor de la elipse es el segmento CD, es perpendicular al segmento AB y corta a este por el medio.
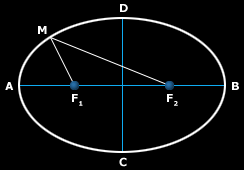
La excentricidad es el grado de aplastamiento de la elipse. Una excentricidad igual a cero representa un círculo perfecto. Cuanto más grande la excentricidad, mayor el aplastamiento de la elipse. Órbitas con excentricidades iguales a uno se denominan parabólicas, y mayores a uno hiperbólicas.
La excentricidad de la elipse puede calcularse de la siguiente manera:
e = F1F2 / AB
Donde e es la excentricidad, F1F2 es a distancia entre los focos y AB es el eje mayor de la elipse. Si la distancia entre los focos F1F2 es cero, como en el caso del círculo, la excentricidad da como resultado cero.
Las órbitas de los planetas son elípticas, presentando una pequeña excentricidad. En el caso de la Tierra el valor de la excentricidad es de 0.017, el planeta de mayor excentricidad es Mercurio con 0.206 (antes era Plutón con 0.248, pero ahora pertenece al grupo de los planetas enanos)
2da Ley - Ley de las Áreas
Las áreas barridas por el radio vector que une a los planetas al centro del Sol son iguales a tiempos iguales.
La velocidad orbital de un planeta (velocidad a la que se desplaza por su órbita) es variable, de forma inversa a la distancia al Sol: a mayor distancia la velocidad orbital será menor, a distancias menores la velocidad orbital será mayor. La velocidad es máximo en el punto más cercano al Sol (perihelio) y mínima en su punto más lejano (afelio).
El radio vector de un planeta es la línea que une los centros del planeta y el Sol en un instante dado. El área que describen en cierto intervalo de tiempo formada entre un primer radio vector y un segundo radio vector mientras el planeta se desplaza por su órbita es igual al área formada por otro par de radio vectores en igual intervalo de tiempo orbital.
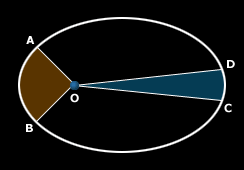
En el gráfico superior: el tiempo que le toma al planeta recorrer del punto A al punto B de su órbita es igual al tiempo que le toma para ir del punto C al D, por tanto, las áreas marcadas OAB y OCD son iguales. Para que esto suceda, el planeta debe desplazarse más rápidamente en las cercanías del Sol (en el foco de la elipse, punto O del gráfico)
3ra Ley - Ley Armónica
Los cuadrados de los períodos orbitales sidéreos de los planetas son proporcionales a los cubos de sus distancias medias al Sol.
El período sidéreo se mide desde el planeta y respecto de las estrellas: está referido al tiempo transcurrido entre dos pasajes sucesivos del Sol por el meridiano de una estrella.
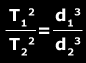
Donde T1 y T2 son los períodos orbitales y d1 y d2 las distancias a las cuales orbitan del cuerpo central. La fórmula es válida mientras las masas de los objetos sean despreciables en comparación con la del cuerpo central al cual orbitan.
Para dos cuerpos con masas m1 y m2 y una masa central M puede usarse la siguiente fórmula:
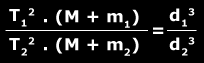
Esta ley fue publicada en 1614 en la más importante obra de Kepler, "Harmonici Mundi", solucionando el problema de la determinación de las distancias de los planetas al Sol. Posteriormente Newton explicaría, con su ley de gravitación universal, las causas de esta relación entre el período y la distancia.
Ejemplo
Supongamos que queremos calcular la distancia entre Sol y Marte. Sabemos que su período orbital es de 1.8809 años. Luego necesitamos tener una referencia conocida, la cual puede ser la Tierra (ya que también órbita al Sol), con un período orbital de 1 año y a una distancia de 1 UA.
Utilizando la tercera ley de Kepler y sin tomar en cuenta las masas de los cuerpos involucrados, podemos calcular el semieje de la órbita de Marte en UA:
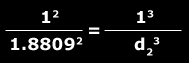
Despejando D2 tenemos que:
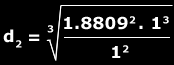
El cálculo nos da como resultado 1.5237 UA. De la misma manera puede calcularse la distancia o el período orbital de los demás planetas.
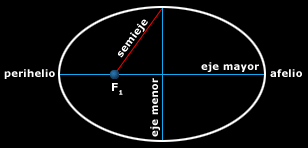
Pero la órbita de Marte es una elipse, por tanto el cálculo nos da el semieje de la órbita (ver gráfico de ejemplo, excentricidad exagerada para mayor claridad). Para calcular el perihelio y el afelio debe introducirse la excentricidad en la ecuación:
Perihelio = a . (1 - e)
Afelio = a . (1 + e)
Donde a es el resultado de nuestro cálculo anterior (semieje), y e representa la excentricidad orbital del planeta, 0.093 en el caso de Marte. Reemplazando y calculando:
Perihelio = 1.5237 . (1 - 0.093) = 1.3819 UA
Afelio = 1.5237 . (1 + 0.093) = 1.6654 UA
El calculo se acerca bastante a los datos reales del planeta (1.381 y 1.666 para el perihelio y afelio, respectivamente)
Podemos calcular también la longitud de los ejes. El eje mayor es, lógicamente, la suma entre la distancia en el perihelio y el afelio: unas 3.0473 U.A. La longitud del eje menor puede calcularse de la siguiente manera:
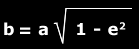
Donde b es la longitud del semieje menor (o sea, la mitad del eje menor), a el semieje de la órbita y e la excentricidad orbital. Calculando con los datos anteriores, tenemos que la longitud del semieje menor es de 1.5171 U.A., lo cual parece lógico al pensar que debe ser mayor que la distancia en el perihelio y menor que la distancia en el afelio. La longitud del eje menor es 1.5171 x 2 = 3.0342 UA
Debe notarse que al calcular el semieje, se está calculando la distancia entre los centros de ambos cuerpos. En el caso de los planetas la diferencia es mínima (un radio planetario más un radio solar) entre el cálculo de la distancia entre los centros y las superficies, pero en el caso de un satélite artificial, la diferencia entre la distancia en el perigeo y el radio vector en ese momento es de un radio planetario (6378 km. en el caso de la Tierra), algo bastante significativo en comparación con la altitud de la órbita del satélite.
Fuentes
- "Elementos de Cosmografía", F. Charola, Kapeluz 1959.
- Notas personales (UNLP, 1998)