Telescopios

Características

Un telescopio es un instrumento óptico que capta cierta cantidad de luz y la concentra en el plano focal para ser ampliada por un ocular, en donde el observador ve los objetos aumentados en tamaño. La cantidad de luz colectada por el instrumento depende del diámetro del objetivo (la apertura). Los oculares los que proporcionan los aumentos al telescopio, y al intercambiar oculares se obtienen diferentes aumentos con el mismo instrumento. El tubo óptico (OTA) se sostiene sobre una montura, la cual provee la capacidad de mover la óptica al punto del cielo deseado. Los distintos diseños de monturas proveen de diferentes funcionalidades, desde las más básicas (movimiento horizontal y vertical), hasta seguimiento de precisión para astrofotografía.

La idea principal en un telescopio astronómico es que brinde al observador la posibilidad de ver objetos débiles o pequeños haciendo uso de la luz que entra en el instrumento. A mayor apertura, mayor será la cantidad de luz y mayor la resolución del instrumento.

Existen tres grandes divisiones entre los telescopios, según el tipo de diseño óptico:

• Reflectores
  Se conforman de un espejo principal (espejo primario u objetivo), el cual fue provisto de cierta curvatura que le permite concentrar la luz en el plano focal. Ejemplo: reflector newtoniano.
• Refractores
  Poseen una o más lentes de cristal óptico (dependiendo del diseño) las cuales concentran la luz en el plano focal. Ejemplo: refractor apocromático.
• Catadióptricos
  Combinan espejos y lentes, estas última para corregir aberraciones ópticas. Ejemplo: Schmidt-Cassegrain.

En astronomía se utilizan todos los diseños, dependiendo principalmente del tamaño y uso del instrumento.

Refractores

El gráfico inferior muestra el funcionamiento simplificado de un típico telescopio refractor de diseño kepleriano. Este es un sistema muy simple donde los rayos convergen en el plano focal y es ahí donde se dispone el ocular para ampliar la imagen. Los rayos de los extremos del objetivo son los que sufren la mayor refracción, mientras que en el eje óptico (o eje de simetría), la luz no es desviada.

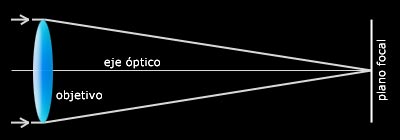
En un telescopio de aficionado idealmente este sistema se encuentra muy mejorado para evitar las aberraciones ópticas que provoca la refracción de la luz, particularmente si el telescopio es de buena calidad. Estos incorporan los llamados dobletes acromáticos, destinados a corregir la aberración cromática, el conocido efecto tipo arco iris en donde las estrellas parecen tener un borde azul y el otro rojo. El doblete acromático dispone de una lente convexa (la misma que en el refractor kepleriano) unida a una cóncava. Diseños más complejos corrigen muy bien las aberraciones, logrando estrellas muy puntuales e imágenes planetarias muy definidas. Un triplete apocromático (compuesto por un conjunto de tres lentes) tiene una mejor corrección cromática, virtualmente eliminando la aberración cromática. Son muy utilizados en astrofotografía.

Una de las ventajas de los telescopios refractores sobre los reflectores es que carecen de obstrucción central (debida al espejo secundario, el cual obstruye parte de la luz y proyecta una sombra sobre el espejo primario). Un instrumento sin obstrucción central ofrece imágenes con un contraste mejorado, algo particularmente interesante en la observación planetaria.

Reflectores

El el esquema inferior se muestra la trayectoria de los rayos en un telescopio reflector simplificado. El espejo primario (objetivo) está especialmente diseñado para reflejar la mayor cantidad de luz posible. A este tipo de espejos es posible brindarles diferentes curvaturas para responder a distintas necesidades (la curvatura influye en la distancia focal, la distancia entre el objetivo y el plano focal). La alta reflectividad se logra a través de un proceso de aluminización realizado en una cámara de vacío, en donde una fina película de aluminio es depositada sobre la superficie del espejo.

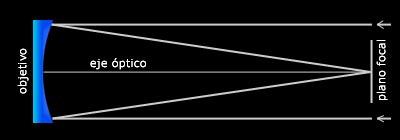
El telescopio reflector es el mas utilizado por los astrónomos profesionales, dado que es posible construir y dar forma a espejos de grandes dimensiones, cosa que no sucede así con los refractores, donde el peso de la lente se vuelve excesivo y la dificultad de producir una lente de calidad de tales dimensiones es casi imposible y muy costoso. El telescopio refractor más grande del mundo posee 1 metro de diámetro, y esta ubicado en el Observatorio Yerkes de la Universidad de California. Fue construido en 1897 por Alvan Clark e Hijos, siendo en su tiempo una pieza clave para la determinación de la forma de nuestra galaxia.

Dentro de la familia de los telescopios reflectores existen varios diseños ópticos. Los más utilizados entre los aficionados son el reflector newtoniano y el reflector Schmidt-Cassegrain.

Reflectores Newtonianos

El reflector Newtoniano dispone de dos espejos, el primario (idealmente parabólico, aunque en pequeñas aperturas usualmente es esférico) y el secundario (más pequeño y plano)

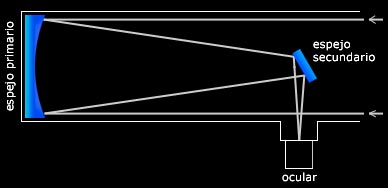
El diseño newtoniano es muy utilizado, dada su simpleza y relativa facilidad de alineado de las partes ópticas (colimación). Otra ventaja es que el objetivo se encuentra protegido en el fondo del tubo óptico, muchas veces evitando que se empañe durante las noches de observación.

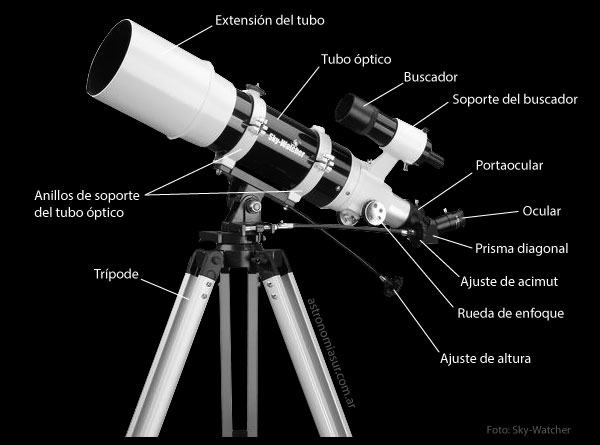
En el esquema superior se detallan las principales partes de un telescopio reflector newtoniano con montura ecuatorial alemana. Diferentes fabricantes y modelos pueden mostrar variaciones, pero las generalidades se mantendrán para este diseño óptico y esta montura.

Los telescopios newtonianos son muy utilizados por su buena relación entre el costo y la apertura. En diámetros grandes la variación elegida por los observadores es la dobsoniano,´en donde el tubo óptico es de diseño newtoniano pero el mismo se sostiene sobre una montura tipo dobsoniana, sencilla, de movimiento vertical y horizontal, usualmente con movimientos manuales. Esto reduce fuertemente los costos, ya que una montura que deba sostener el peso de un espejo grande debe ser muy robusta.

Catadióptricos

En el diagrama inferior se muestra el diseño de un telescopio catadióptrico del tipo Schmidt-Cassegrain. Este diseño es compacto en comparación con la focal brindada. Es un telescopio apto tanto para la observación planetaria como para objeto de cielo profundo, sobre todo si muestran tamaños aparentes pequeños, ya que las focales tienden a ser grandes.

Los Schmidt-Cassegrain poseen un espejo primario parabólico con una perforación en su centro, para recibir la luz proveniente del espejo secundario, el cual es convexo. La función de la placa correctora es corregir la luz antes de que llegue al espejo primario. Este luego la envía al secundario (que es convexo), el cual tiene la función de recibir rayos en diferentes ángulos y reflejarlos todos paralelos hasta el plano focal, lugar donde se ubica el ocular.

La imagen superior ilustra un telescopio Schmidt-Cassegrain sobre una montura altacimutal computarizada con un sistema GOTO (el telescopio se maneja desde un control, hand control)

Definiciones y Fórmulas Útiles

Conociendo los datos del instrumento y sus accesorios podremos calcular fácilmente varios parámetros útiles, como el aumento, campo visual real, resolución, etc. A continuación se detallan las sencillas y útiles fórmulas.

Diámetro (D)

El diámetro o apertura de un telescopio está referido al tamaño del objetivo (lente o espejo) por el cual ingresa la luz al instrumento. Por uso y costumbre, se suelen utilizar dos unidades diferentes, los milímetros y las pulgadas. Solo debe recordarse que 1 pulgada equivale a 2.54 cm, y al realizar cálculos mantener todos los valores en las mismas unidades (milímetros como recomendada).

Distancia Focal (F)

La distancia focal es distancia comprendida entre el objetivo del telescopio (sea un reflector o refractor) y el plano focal del mismo. Esta medida cambia con el diseño del objetivo (por ejemplo, con la curvatura del espejo) Este dato es intrínseco de cada instrumento. La unidad más utilizada para la distancia focal son los milímetros. Es un dato importante para calcular los aumentos y la razón focal.

Razón Focal (F/D)

La razón focal (F/D) es un valor que relaciona la focal con el diámetro, y brinda un dato de cuan luminoso es el telescopio para astrofotografía. Cuanto más corta es la distancia focal y mayor el objetivo, mas luminoso será el telescopio. Este concepto no es aplicable en la observación visual, ya que si observamos con el mismo diámetro de objetivo y los mismos aumentos, la imagen será igual de luminosa sin importar la razón focal del sistema óptico (podrá tener una escala diferente, pero si pensamos el brillo por unidad de área, si el diámetro es el mismo y los aumentos son los mismos, los dos instrumentos darán una imagen igual de luminosa)

Para calcular el F/D de un telescopio solo hay que dividir la distancia focal por el diámetro del objetivo, todo en las mismas unidades:

F/D = F [mm] / D [mm]

Ejemplo: un telescopio reflector de 203 mm de diámetro y 1000 mm de distancia focal.

F/D = 1000 mm / 203 mm

Resultado:

F/D = 4.9

Aumentos

Los aumentos en un telescopio son provistos por los oculares, los cuales actúan como lupas sofisticadas, ampliando la imagen que el objetivo ha concentrado en el plano focal para así poder ser observada con el ojo. Los aumentos dependen de la distancia focal del telescopio y de la focal de los oculares, e intercambiando oculares de diferentes focales se obtendrán diferentes aumentos. La cantidad de aumentos indica cuanto más grande se ha ampliando la imagen con respecto a no utilizar ningún instrumento (a simple vista) y se calcula sencillamente dividiendo la focal del telescopio por la focal del ocular. Oculares de focales cortas darán más aumentos.

A = F_T [mm] / F_O [mm]

Ejemplo: un telescopio de 1000 mm de distancia focal utilizando un ocular de 25 mm.

A = 1000 mm / 25 mm

Resultado:

A = 40x

Los aumentos son una magnitud sin unidad que llevan una "x" al final que se lee "por" (siguiendo el ejemplo, debe leerse "cuarenta por" o "cuarenta aumentos" directamente).

Existe un límite útil para los aumentos de un telescopio, el cual depende del diámetro del objetivo: a mayor diámetro mayor será la posibilidad de utilizar grandes ampliaciones. Si se sobrepasa el límite recomendado se hace imposible obtener imágenes nítidas y aparece la llamada "mancha de difracción". Este límite viene dado por la física involucrada en la óptica. La fórmula más utilizada simplemente multiplica por 2.3 el diámetro del objetivo en milímetros. Algunos autores utilizan 2.5 como factor.

A_Max = 2.3 x D

Ejemplo: un telescopio de 203 mm de apertura.

A_Max = 2.3 x 203 mm

Resultado:

A_Max = 467x

Este límite es teórico y las condiciones de observación (particularmente la estabilidad de la atmósfera) normalmente marcan como máximos aumentos valores menores.

Resolución

Se llama resolución (o poder separador) a la capacidad de un telescopio de mostrar diferenciados a dos objetos que se encuentran muy juntos. Hay diferentes aproximaciones al concepto, pero una de las más utilizadas en la del llamado límite de Dawes. Esta medida se da en segundos de arco y se relaciona con diámetro del objetivo, dado que a mayor diámetro mayor es el poder separador del instrumento.

Cuando se habla, por ejemplo, de una resolución de 1 segundo de arco, se está refiriendo a que esa es la mínima separación que deben tener dos objetos puntuales para ser distinguibles entre sí. Hay que destacar que no depende de la ampliación utilizada (no se aumenta la resolución por utilizar mayores aumentos), ya que un instrumento posee cierto poder separador intrínseco definido principalmente por la apertura.

El límite de Dawes puede calcularse dividiendo 116 por el diámetro del objetivo en milímetros (el número 116 proviene de medidas empíricas, el uso de una longitud de onda específica, y conversiones para utilizar milímetros)

R = 116 / D

Ejemplo: un telescopio de 203 mm de apertura.

R = 116 / 203 mm

Resultado:

R = 0.57"

Debe tenerse en cuenta que esta será la resolución teórica del instrumento, y que en condiciones reales puede ser muy difícil de alcanzar, ya sea por limitaciones atmosféricas o imperfecciones ópticas.

Magnitud Límite

A mayor diámetro, mayor será el poder recolector de luz, lo que permitirá observar objetos más débiles. La siguiente fórmula provee de una guía para saber hasta qué magnitud límite estelar alcanza el instrumento, pero el valor real dependerá también de factores como la calidad de las ópticas utilizadas, la oscuridad del sitio de observación, la adaptación de nuestros ojos a la oscuridad y la cantidad de aumentos utilizados (para el caso de las estrellas a mayor aumento mayor será el contraste con el fondo de cielo).

M_Límite = 7.5 + 5 x Log D [cm]

Algunos autores utilizan 7.7 como constante, en vez de 7.5. Ejemplo: un telescopio de 203 mm de apertura (20.3 cm).

M_Límite = 7.5 + 5 x Log 20.3

M_Límite = 7.5 + 6.54

Resultado:

M_Límite = 14.04

Debe notarse que el dato obtenido es válido para magnitudes estelares (estrellas, y otros objetos que se comporten como puntuales) y no para objetos extensos (que muestran un área) como galaxias, nebulosas o cúmulos globulares. En los catálogos de objetos de cielo profundo el dato que aparece como magnitud normalmente es el de magnitud integrada, pero al tener una superficie el brillo se distribuye en ella, y son otras las consideraciones que deben tenerse (por ejemplo, el tamaño aparente del objeto influye en las posibilidades de detección).

Campo Visual (FOV)

Se denomina campo visual (FOV) al diámetro angular (se mide en grados) de cielo observado a través del telescopio. Para calcularlo se debe dividir el campo aparente del ocular (AFOV), un dato intrínseco que depende del diseño óptico de ocular, por los aumentos (A) provistos con ese ocular.

FOV = AFOV / A

Ejemplo: un ocular de 60º de campo aparente que esté proveyendo de 40x (40 aumentos)

FOV = 60º / 40

Resultado:

FOV = 1.5º

Siguiendo el ejemplo, sabiendo que la Luna tiene una tamaño aparente de 0.5º, un campo visual de 1.5º equivale a 3 veces el diámetro de la luna llena. Ver más sobre oculares.