Coordenadas

Introducción

Al igual que para ubicar un punto geográfico sobre la superficie de la Tierra se utiliza un sistema de coordenadas compuesto por dos valores (latitud y longitud), para localizar un objeto sobre la esfera celeste también existen varios sistemas, basados en diferentes planos, que permiten saber la posición del objeto. Aquí estudiaremos los dos más utilizados:

• Coordenadas Altacimutales
• Coordenadas Ecuatoriales

Estos dos sistemas tienen una diferencia fundamental: mientras que las coordenadas ecuatoriales permiten que dos observadores distantes puedan localizar un mismo objeto (el valor de las coordenadas no cambia), las coordenadas altacimutales son locales (los valores cambian al cambiar la ubicación geográfica y, generalmente, el momento de la observación). Más adelante se detallará cada sistema.

Ángulos

Para expresar la distancia entre dos objetos sobre la esfera celeste se utilizan ángulos: el ángulo que se forma entre el observador y los dos puntos de la esfera celeste es la distancia angular entre los objetos. Estos ángulos se miden en grados, minutos y segundos (o su equivalente en grados decimales, ver calculadora)

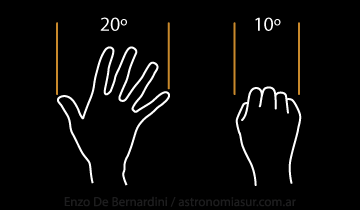
Para estimar sin instrumentos una distancia angular se puede utilizar el método aproximado de extender el brazo y abrir la palma de la mano: la distancia entre el extremo de los dedos pulgar y meñique forma un ángulo de unos 20º sobre la esfera celeste. El puño cerrado equivale a unos 10º.

Coordenadas Altacimutales

También llamadas coordenadas horizontales, las coordenadas altacimutales utilizan dos valores para ubicar la posición de un objeto sobre la esfera celeste:

• Altura (h)
• Acimut (A)

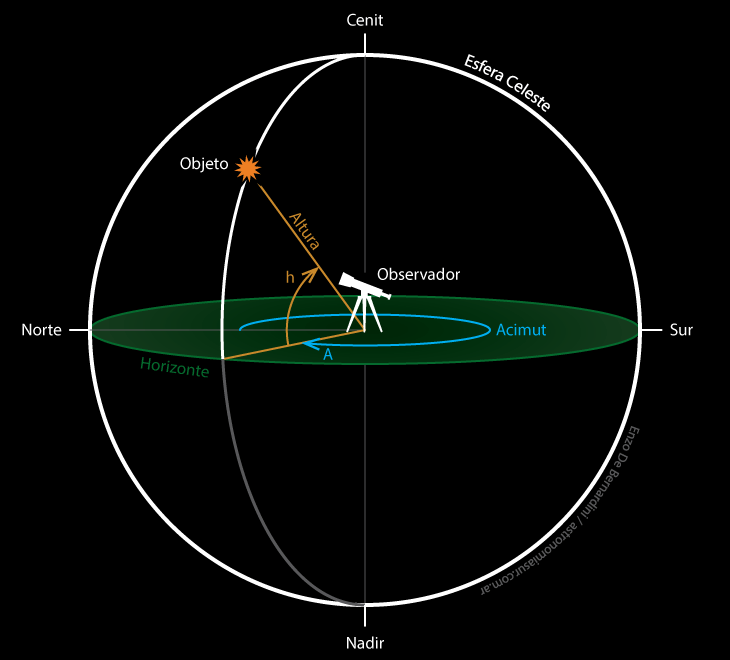
La altura (h) se mide desde el horizonte (0º) hasta el cenit (90º), por tanto el valor de la altura será igual al ángulo que forme el objeto observado con el horizonte. Para objetos por debajo del horizonte la altura es negativa. El punto opuesto al cenit, a -90º de altura, se lo conoce como nadir.

El acimut (A), se mide en grados, de 0º a 360º, comenzando desde el punto cardinal norte (0º) y hacia el este (90º). De esta forma un objeto que se encuentre directamente al sur tendrá un acimut de 180º, uno al oeste de 270º, etc.

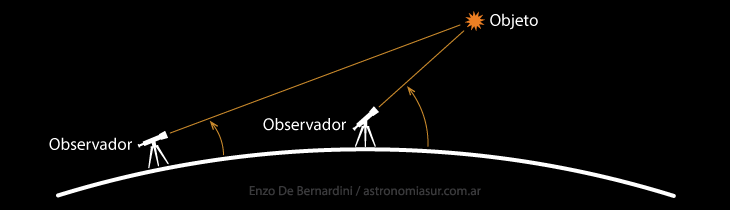
Al tratarse de un sistema de coordenadas locales el valor de altura y acimut para un objeto dependerá de la posición del observador y, por lo general, del momento de la observación. Como muestra la figura inferior, dos observadores con diferentes ubicaciones sobre la superficie de la Tierra medirán un ángulo de altura diferente para un mismo objeto. La misma idea se aplica para el valor del acimut. A su vez, un mismo observador que vuelva a medir la altura y acimut de un objeto luego de cierto tiempo verá que los valores han cambiado (por ejemplo, el objeto puede haber aumentado en altura al pasar el tiempo)

Esfera Celeste

Los planos fundamentales de la esfera celeste, en los que se basan los diferentes sistemas de coordenadas astronómicas son los siguiente:

• Ecuador Celeste
  Es la proyección del ecuador terrestre sobre la esfera celeste.
• Polos Celestes
  Hay dos, el polo norte celeste (NCP) y el polo sur celeste (SCP). Son la proyección del eje de rotación de la Tierra en la esfera celeste.
• Eclíptica
  Se define como el plano que forma la trayectoria media del centro de gravedad de la Tierra. Es la línea por la cual se mueve el Sol a lo largo del año. Se encuentra inclinada en 23º 27' con respecto al ecuador celeste (ε, la oblicuidad de la eclíptica, es el valor de la inclinación del eje de rotación de la Tierra). El punto en donde la eclíptica cruza el ecuador celeste de sur a norte se denomina punto gamma (γ), siendo el origen de la ascensión recta (R.A.) en el sistema de coordenadas ecuatoriales celestes.

Coordenadas Ecuatoriales

Las coordenadas ecuatoriales celestes tienen como plano fundamental el ecuador celeste, el cual, como se ha visto, es la proyección del ecuador terrestre sobre la esfera celeste. Este sistema utiliza los siguientes valores para ubicar un objeto sobre la esfera celeste:

• Ascensión Recta (R.A., α)
• Declinación (Dec., δ)

La ascensión recta (α) se mide sobre el ecuador celeste desde el punto gamma (o punto vernal) hacia el este, de 0 a 24 horas (1 hora equivale a 15 grados) El punto gamma (γ) es el punto en el que la eclíptica cruza al ecuador celeste de sur a norte. La declinación (δ) es medida en grados desde el ecuador celeste hacia los polos, positiva hacia el norte y negativa hacia el sur. El ecuador celeste tiene declinación igual a cero grados, y los polos declinaciones +90º (polo norte celeste) y -90º (polo sur celeste).

El punto gamma se localiza en una de las dos intersecciones del ecuador celeste con la eclíptica, la línea por donde de observa desplazarse al Sol durante el año. En el instante del equinoccio de otoño (hemisferio sur) el Sol posee una ascensión recta de 0^h 0^m 0^s.

En el gráfico inferior se muestra una esfera celeste, construida para una latitud media sur, donde el polo elevado es el polo sur celeste.

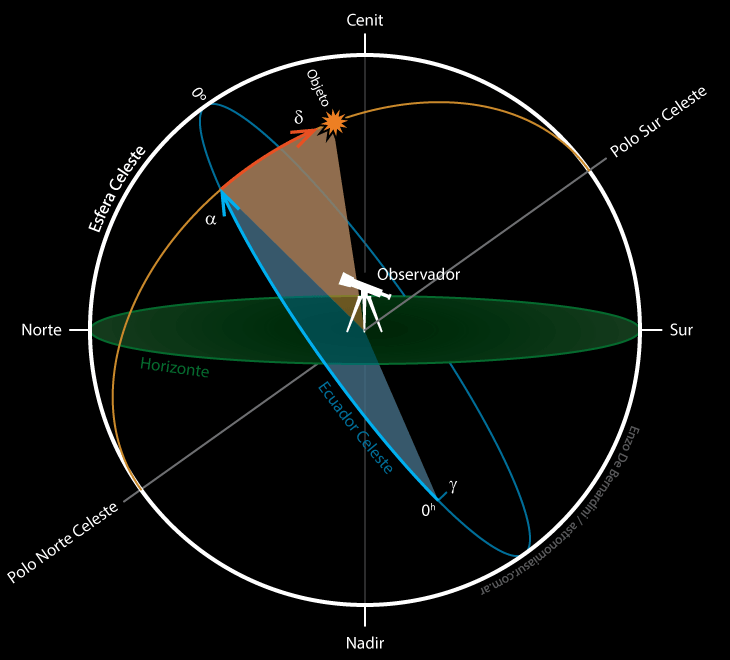
La altura del polo elevado es igual a la latitud (φ) del lugar de observación, y se encuentra directamente en dirección sur en el hemisferio sur, y norte en el hemisferio norte. El eje de ascensión recta de una montura ecuatorial debe apuntar al polo elevado (para así ser paralelo al eje de rotación de la Tierra). Esto permite al telescopio compensar el movimiento de rotación de la Tierra (para ser más precisos la velocidad del telescopio es sidérea: no solo se compensa el movimiento de rotación de la Tierra, sino el de traslación de nuestro planeta alrededor del Sol).

Estudiando el gráfico podemos ver que existe un grupo de estrellas que nunca quedan por debajo del horizonte al rotar la esfera celeste. A estas estrellas se las denomina circumpolares y se encuentran en el llamado casquete circumpolar. La declinación límite a la que debe encontrarse una estrella para ser circumpolar de ±90º menos la latitud (φ) de observación, utilizando -90º para el hemisferio sur y +90º para el hemisferio norte:

δ_max = ±90º - φ

De esta forma, por ejemplo, para una latitud sur de 35º obtenemos que la máxima declinación para que una estrella sea circumpolar será de -55º de declinación.

δ_max = -90º - (-35º)

δ_max = -55º

Esta declinación se corresponde aproximadamente a la de la estrella Gacrux (γ Crucis), la estrella más al norte de la constelación Crux (Cruz del Sur), lo que indica que está constelación nunca se oculta por debajo del horizonte desde latitudes como la de Buenos Aires, Santiago, Montevideo o Sydney.

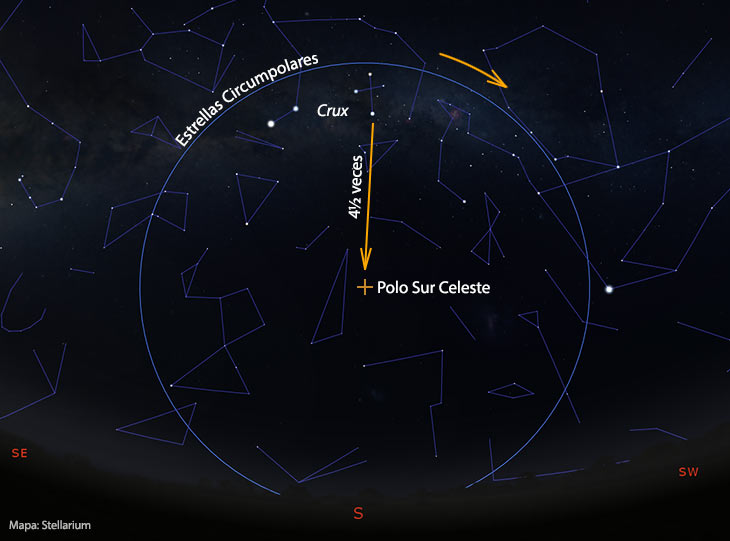
De forma análoga, también existe un grupo de estrellas que nunca asoman por encima del horizonte. Siguiendo el ejemplo, si el observador se encuentra en una latitud media sur habrá un casquete circumpolar polar norte que nunca es visible. La declinación máxima de estas estrellas será igual, pero en signo opuesto, al del casquete circumpolar sur (+55º para el ejemplo).